1365. Dijkstra alqoritmi

İstiqamətlənmiş çəkili qraf verilir. s təpəsindən f təpəsinə qədər ən qısa yolu tapın.

Giriş verilənləri. İlk sətir üç n, s və f (1 ≤ n ≤ 100, 1 ≤ s, f ≤ n) ədədlərini ehtiva edir, burada n qrafın təpələrinin sayıdır. Qrafın qonşuluq matrisini əks etdirən növbəti n sətrin hər biri n ədəd ehtiva edir, burada i sətri və j sütunu i-dən j-yə olan tili əks etdirir: -1 iki təpə arasında tilin olmadığını bildirir və mənfi olmayan hər hansı ədəd – verilmiş tilin çəkisini bildirir. Matrisin əsas diaqonalı həmişə sıfır qiymətlərini ehtiva edir.

Çıxış verilənləri. Tələb olunan məsafəni və ya verilmiş təpələr arasında yol yoxdursa -1 verməli.

Giriş verilənlərinə nümunə

3 1 2

0 -1 2

3 0 -1

-1 4 0

Çıxış verilənlərinə nümunə

6

HƏLLİ

qraflar – Dijkstra alqoritmi

Alqoritmin analizi

Məsələnin həlli üçün Dijkstra alqoritmini reallaşdırmaq lazımdır.

Nümunə

Misalda verilmiş qraf aşağıdakı şəkildədir:

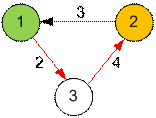
1 təpəsindən 2 təpəsinə ən qısa yol 2 + 4 = 6-dır.

Alqoritmin reallaşdırılması

Dijkstra alqoritmini prioritetli növbə vasitəsilə reallaşdırırıq. Növbənin elementləri cütlüklərdir (mənbədən olan məsafə və təpənin nömrəsi). Beləliklə, növbədə birinci olaraq həmişə mənbəyə yaxın olan təpə (Dijkstra alqoritminin icra ediləcəyi başlanğıc təpə) olacaq. Bu cütlüyü (Dist, Vertex) ehtiva edən Prior sinfini elan edək. Böyük və kiçik operatorlarını təyin edək: o cütlük kiçik sayılır ki, mənbəyə qədər olan məsafə (Dist) ən kiçik olsun.

class Prior

{

public:

int Dist, Vertex;

Prior(int Dist, int Vertex) : Dist(Dist), Vertex(Vertex) {}

int operator< (const Prior &a) const

{

return Dist < a.Dist;

}

int operator> (const Prior &a) const

{

return Dist > a.Dist;

}

};

Qraf sinfini elan edək. O təpə nöqtələrinin n sayını ehtiva edir və g qonşuluq siyahısı ilə verilir.

class Graph

{

public:

int n;

vector<vector<int> > g;

Graph(int n = 1) : n(n)

{

g.assign(n,vector<int>(n));

}

Len çəkili istiqamətlənmiş til əlavə etmə funksiyası.

void AddEdge(int From, int To, int Len)

{

g[From][To] = Len;

}

Dijkstra alqoritmi Source təpəsindən icra edilir. İkinci arqument kimi ən qısa məsafələr massivi time verilir.

void Dijkstra(int Source, vector<int> &dist)

{

priority_queue<Prior, vector<Prior>, greater<Prior> > pq;

Növbəyə cütlüyü (0, Source) yerləşdirək, başlanğıc təpədən onun özünə qədər olan dist[Source] məsafəsinin 0-a bərabər olduğunu hesab edirik.

pq.push(Prior(0,Source)); dist[Source] = 0;

while(!pq.empty())

{

int v = pq.top().Vertex;

int d = pq.top().Dist; pq.pop();

Növbənin başından cütlüyün (v, d) çıxarılmasının yalan olduğunu yoxlayırıq.

if (d > dist[v]) continue;

v ilə qonşu olan to təpəsinə baxırıq. (v, to) tilinin qısaltmasını verməyə çalışırıq. Əgər til qısadırsa, növbəyə yeni cütlüyü (dist[to], to) daxil edirik.

for(int to = 0; to < n; to++)

if (dist[to] > dist[v] + g[v][to])

{

dist[to] = dist[v] + g[v][to];

pq.push(Prior(dist[to],to));

}

}

}

};

Qraf göstəricisi təyin edək.

Graph *g;

Proqramın əsas hissəsi. Giriş verilənlərini oxuyuruq. g qrafını quraq. Ən qısa məsafələr üçün dist massivini verək. Başlanğıc və son təpələr 1-dən başlayaraq nömrələmə şərti ilə verilir. Buna görə də onlardan 1 çıxırıq.

scanf("%d %d %d",&n,&s,&f);

s--; f--; g = new Graph(n);

dist = vector<int>(n,INF);

Giriş qrafını oxuyuruq. Əgər tilin uzunluğu -1-ə bərabərdirsə (til yoxdursa), onda onu müsbət sonsuzluğa bərabər götürürük.

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

{

scanf("%d",&Len);

if (Len < 0) Len = INF;

g->AddEdge(i,j,Len);

}

s təpəsindən Dijkstra alqoritmini icra edirik.

g->Dijkstra(s,dist);

Nəticəni veririk.

if (dist[f] == INF) printf("-1\n");

else printf("%d\n",dist[f]);

Prior sinfinin aradan qaldırılması

Əgər növbənin elementlərini tam ədədlər cütlüyü (mənbədən təpələrə qədər olan məsafə, təpənin nömrəsi) = (dist[v], v) kimi saxlayarıqsa, Prior sinfini daxil etməyə bilərik. Əgər bu ədədlər int tipində olarlarsa, onda göstərilən cütlüyü long long tipində dist[v] * 2³² + v ədədi ilə kodlaşdıra bilərik. Onda Dijkstra alqoritmində növbə long long tipində ədədlərlə işləyəcək.

void Dijkstra(int Source, vector<int> &dist)

{

priority_queue<long long, vector<long long>, greater<long long> > pq;

pq.push(Source); dist[Source] = 0;

while(!pq.empty())

{

long long PQnode = pq.top(); pq.pop();

PQnode – cütlüyün kodudur. Kiçik iki bayt v təpəsinin nömrəsini saxlayır, böyük iki bayt isə cütlüyün növbəyə əlavə edildiyi an mənbədən v təpəsinə ən qısa d məsafəsini saxlayır.

int v = (int)PQnode;

int d = PQnode >> 32;

if (d > dist[v]) continue;

for(int to = 0; to < n; to++)

if (dist[to] > dist[v] + g[v][to])

{

dist[to] = dist[v] + g[v][to];

Cütlüyün (dist[to], to) kodu (dist[to] << 32) + to ədədi olacaq.

pq.push(((long long)dist[to] << 32) + to);

}

}

}